微分概念中的反例

反例: 不能是某个函数导数的函数.

由达布介值定理, 这样的函数不能有第一类间断点, 所以符号函数即为反例.

反例: 仅在一点可导的函数.

$$f(x)=\begin{cases} x^{2}, & x\in\QQ\\ 0, & x\not\in\QQ \end{cases}$$

只在$x=0$处可导.

其它例子

设函数$f:\RR\to\RR$定义如下:

$$f(x)=\begin{cases} x, & x\in\QQ,\\ -x, & x\not\in\QQ. \end{cases}$$

则$f$只在一点处连续. 设$g:\RR\to\RR$定义为

$$g(x)=f(x)x.$$

则$g$只在$x=0$处可导. 这是因为

$$g'(0)=\lim_{h\to0}\frac{f(h)h-f(0)0}{h}=\lim_{h\to0}f(h)=0.$$

如果$g$在某个$x\ne0$处连续, 则$f(x)=g(x)/x$在点$x$处也连续, 而这是不可能的.

反例: $f(x)$在点$x_{0}$可导, 不一定有$f(x)$在$x_{0}$点的领域内的每个点处可导.

同上

反例: 在任何点的导数都不存在的函数.

$$f(x)=\begin{cases} x, & x\in\QQ\\ 0, & x\not\in\QQ \end{cases}$$

另外还有处处连续处处不可导的Weierstrass函数.

反例: $f(x)$在一点可导必然在该点连续, 反之不真.

同上, 或者$f(x)=|x|$处处连续, 但在$x=0$处不可导, 又比如

$$f(x)=\begin{cases} x, & x\le0,\\ x\sin\frac{\pi}{x}, & x>0, \end{cases}$$

在$x=0$处连续, 但在$x=0$处不可导.

反例: 在$n$个点($n\in\NN$)处不可导的连续函数.

$f(x)=\left(|x-a_{1}|+|x-a_{2}|+\cdots+|x-a_{n}|\right).$

反例: 处处连续处处不可导函数.

处处连续, 无处单调, 处处不可导函数:

$$f(x)=\sum_{n=1}^{\infty}f_{n}(x)=\sum_{n=1}^{\infty}\frac{f_{1}(4^{n-1}x)}{4^{n-1}},\quad x\in\RR,$$

其中

$$f_{1}(x)=\begin{cases} |x|, & |x|\le\frac{1}{2}\\ f_{1}(x+n), & \mathrm{otherwise,} \end{cases}$$

反例: 函数可导, 但导函数不一定连续.

构造反例需要注意达布的介值定理,

$$f(x)=\begin{cases} x^{2}\sin\frac{1}{x}, & x\ne0\\ 0, & x=0, \end{cases}$$

$f(x)$是处处可导的, 但$f’(x)$在$x=0$处是第二类间断点.

反例: 若$f(x)$, $g(x)$均在$x_{0}$点不可导, 但$f(x)+g(x)$有可能在$x_{0}$点可导.

$f(x)=\frac{x+|x|}{2}$, $g(x)=\frac{x-|x|}{2}$.

反例: 若$f(x)$, $g(x)$均在$x_{0}$点不可导, 但$f(x)\cdot g(x)$有可能在$x_{0}$点可导.

$f(x)=g(x)=|x|$.

反例: 若$f(x)$, $g(x)$其中之一在$x_{0}$点不可导, 则它们的积$f(x)\cdot g(x)$的可导性不确定.

$f(x)=x$, $g(x)=|x|$; $f(x)=1$, $g(x)=|x|$.

反例: 若$f(x)$在点$x=g(x_{0})$可导, 而$g(x)$在$x_{0}$点不可导, 则函数$F(x)=f\left[g(x)\right]$在点$x_{0}$的可导性不确定.

$f(x)=x^{2}$, $g(x)=|x|$; $f(x)=x$, $g(x)=|x|$.

反例: 若$f(x)$在点$x=g(x_{0})$不可导, 而$g(x)$在点$x_{0}$可导, 则$F(x)=f\left[g(x)\right]$在点$x_{0}$处的可导性不确定.

$f(x)=|x|$, $g(x)=x^{2}$; $f(x)=|x|$, $g(x)=x$.

反例: 若$f(x)$在点$x=g(x_{0})$不可导, $g(x)$在$x_{0}$处也不可导, 则$F(x)=f\left[g(x)\right]$在点$x_{0}$处的可导性不确定.

$f(x)=2x+|x|$, $g(x)=\frac{2}{3}x-\frac{1}{3}|x|$; $f(x)=g(x)=|x|$.

上面第一个的例子可以通过单调函数的反函数来构造, 这样的函数是大量存在的.

反例: 若$f(x)$在有限区间$(a,b)$上可微, 且$\lim_{x\to a}f(x)=\infty$, 但不一定有$\lim_{x\to a}f’(x)=\infty$.

$f(x)=\frac{1}{x}+\cos\frac{1}{x}$, $x\in\left(0,\frac{\pi}{2}\right)$,
这时候$f’(x)=-\frac{1}{x^{2}}+\frac{1}{x^{2}}\sin\frac{1}{x}$.

反例: 若$f(x)$在有限区间$(a,b)$上可微, 且$\lim_{x\to a}f’(x)=\infty$, 但不一定有$\lim_{x\to a}f(x)=\infty$.

$f(x)=\sqrt[3]{x}$, $x\in(0,b)$, $b>0$, 此时$f’(x)=\frac{1}{3\sqrt[3]{x^{2}}}$.

反例: 若$f(x)$在$(x_{0},+\infty)$上可微, 且有$\lim_{x\to+\infty}f(x)$存在, 但$\lim_{x\to+\infty}f’(x)$不一定存在.

$f(x)=\frac{\sin x^{2}}{x}$, $x\in\left(0,+\infty\right)$, 此时$f’(x)=2\cos x^{2}-\frac{\sin x^{2}}{x^{2}}$.

反例: 若有界函数$f(x)$在$(x_{0},+\infty)$上可微, 且$\lim_{x\to+\infty}f’(x)$存在, 但$\lim_{x\to+\infty}f(x)$不一定存在.

$f(x)=\cos(\ln x)$, $f’(x)=-\frac{\sin\ln x}{x}$; $f(x)=\ln x$,

反例: 定义在无限区间$I$上的函数$f(x)$, 在$I$上无界, 但$f’(x)$在$I$上不一定无界.

$f(x)=\ln x$.

反例: 若$f(x)>g(x)$, 但不一定有$f’(x)>g’(x)$.

在相差一个常数的原函数中, 反例随处可见.

反例: (分析) 若$f(x)$是可微函数, 且$f’(x)$在$[a,+\infty)$上有界, 则$f(x)$在$[a,+\infty)$上一致连续, 但反之不真.

$f(x)=\sqrt{x}$, $x\in[0,+\infty)$.

反例: 单调函数的导数未必单调.

显然, 导数处处存在的情况下应当处处非负, 与单调性无关. $f(x)=x+\sin x$, $x\in(0,+\infty)$.

反例: 若函数$f(x)$在点$x_{0}$点可导, 则曲线$y=f(x)$在点$(x_{0},f(x_{0}))$存在切线. 但若$f(x)$在点$x_{0}$不可导, 曲线$y=f(x)$在点$(x_{0},f(x_{0}))$处也可能有切线.

$f(x)=\sqrt[3]{x}$.

反例: $f(x)$在点$x_{0}$处连续, 但在$x_{0}$点处既无右导数又无左导数.

$$f(x)=\begin{cases} x\sin\frac{1}{x}, & x\ne0\\ 0, & x=0. \end{cases}$$

反例: 函数$f(x)$有有限极限$\lim_{x\to a}f’(x)$, 但$f(x)$没有单侧导数$f’(a+0)$, $f’(a-0)$.

$$f(x)=\begin{cases} \arctan\frac{1+x}{1-x}, & x\ne1,\\ 0, & x=1. \end{cases}$$

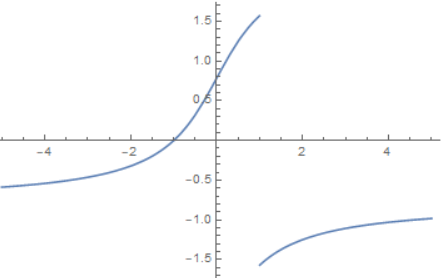
这个函数在$f(1+0)=-\frac{\pi}{2}$, $f(1-0)=\frac{\pi}{2}$, 有跳跃间断点. $f’(x)=\frac{1}{1+x^{2}}$,
所以$\lim_{x\to1}f’(x)=\frac{1}{2}$, 但$f’(1+0)$和$f’(1-0)$都不存在.

反例: 可导的逆

若函数$f(x)$可导, 则

$$\lim_{n\to\infty}n\left[f\left(x+\frac{1}{n}\right)-f(x)\right]=f'(x),\quad n=1,2,\cdots,$$

但反之不成立.

$$f(x)=\begin{cases} 1, & x\in\QQ\\ 0, & x\not\in\QQ, \end{cases}$$

当$x$为有理数时, $x+\frac{1}{n}$是有理数, 所以上面的极限为$0$, 但$f(x)$在有理点不连续也不可导.

反例: 处处可导, 但导函数不连续

处处可导, 但导函数不连续: 定义函数$f$如下

$$f(x)=\begin{cases} x^{2}\sin\left(\frac{1}{x}\right), & x\ne0\\ 0, & x=0. \end{cases}$$

证明

对于$x\ne0$, 则按照求导法则, $f’(x)=2x\sin\left(\frac{1}{x}\right)-\cos\left(\frac{1}{x}\right)$.
因为$f’\left(\frac{1}{2k\pi}\right)\to-1$, $f’\left(\frac{1}{(2k+1)\pi}\right)\to1$, 所以$f’(x)$在$x\to0$时没有极限. 所以

$$\lim_{x\to0}f'(x)$$

不存在.

然而按照导数的定义, $f’(0)$却是存在的:

$$f'(0)=\lim_{h\to0}\frac{f(h)-f(0)}{h}=\lim_{h\to0}h\sin\left(\frac{1}{h}\right),$$

由于$-1\le\sin\left(\frac{1}{h}\right)\le1$, 所以差商满足

$$-\left|h\right|\le h\sin\left(\frac{1}{h}\right)\le\left|h\right|,\qquad\forall h\ne0.$$

但是, 因为$\lim_{h\to0}-\left|h\right|=\lim_{h\to0}\left|h\right|=0$, 所以$\lim_{h\to0}h\sin\left(\frac{1}{h}\right)=0$. 下图表示函数$f$的图像,

反例: 函数$f(x)$的导数$f’(x)$有限, 但$f’(x)$在一个闭区间上却无界.

反例的意思是$f(x)$在任何点$x$处的导数都是有限数值, 但$f’(x)$仍然无界的情况

$$f(x)=\begin{cases} x^{2}\sin\frac{1}{x^{2}}, & x\ne0,\\ 0, & x=0, \end{cases}$$

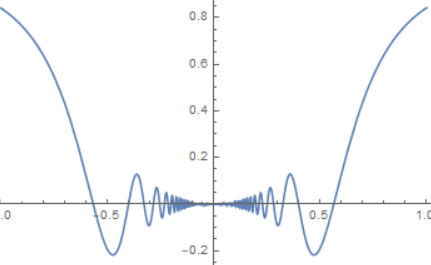
则

$$f'(x)=\begin{cases} 2x\sin\frac{1}{x^{2}}-\frac{2}{x}\cos\frac{1}{x^{2}}, & x\ne0\\ 0, & x=0 \end{cases}$$

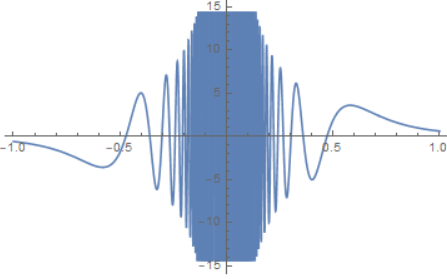
反例: 罗尔定理

若$f(x)$满足:

1. 在闭区间$[a,b]$上连续;

2. 在开区间$(a,b)$内可导;

3. $f(a)=f(b)$;

则在开区间$(a,b)$内至少存在一点$\xi$, 使得

$$f'(\xi)=0$$

定理的条件缺一不可.

不满足1的反例:

$$f(x)=\begin{cases} \frac{1}{x}, & x\ne0,\\ 1, & x=0. \end{cases}$$

在$a=0$, $b=1$的情况

不满足2的反例: $f(x)=|x|$, $x\in[-1,1]$.

不满足3的反例: $f(x)=\ln x$, $x\in[1,2]$.

定理中的零点不唯一, 大多数三角函数皆为例子.

反例: 拉格朗日中值定理

若$f(x)$满足以下条件:

1. 在闭区间$[a,b]$上连续;

2. 在开区间$(a,b)$可导;

则在开区间$(a,b)$内至少有一点$\xi$, 使得

$$f'(\xi)=\frac{f(b)-f(a)}{b-a}.$$

定理的条件缺一不可.

不满足1的反例: $f(x)=\frac{1}{x}$, $x\in(0,1)$, 但$f$在$0$或$1$的取值使$f$不连续时.

不满足2的反例: $f(x)=|x|$, $x\in[-1,2]$. 选择这样的区间是为了和罗尔定理区别开来.

反例: 拉格朗日中值定理的逆

若$f(x)$在闭区间$[a,b]$上连续, 开区间$(a,b)$内可导, 则对于$(a,b)$内的任意两点$x_{1}$, $x_{2}$都有$x_{1}$与$x_{2}$之间的$\xi$, 使得

$$f'(\xi)=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}},\quad\xi\in(x_{1},x_{2}).$$

但若$f(x)$在开区间内有连续导数$f’(x)$, 对于$(a,b)$内任意的$\xi$, 不一定有两点$x_{1}$,
$x_{2}$, 使得

$$f'(\xi)=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}},\quad\xi\in(x_{1},x_{2}).$$

如: $f(x)=x^{3}$, 取$\xi=0$.

反例: Cauchy中值定理

若$f(x)$, $g(x)$在$[a,b]$上连续, 在$\left(a,b\right)$内可导, $g’(x)$在$(a,b)$内每一点都不为零, 则至少存在一点$\xi\in(a,b)$, 使得:

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}.$$

1. $f,g$之一在$[a,b]$上不连续的反例:

   $$f(x)=\begin{cases} x, & x\ne0,\\ 2, & x=0, \end{cases}\quad g(x)=x.$$

   取$a=0$, $b=1$.

2. $f,g$之一在$(a,b)$内不可导的反例: $f(x)=|x|$, $g(x)=x$, $a=-1$, $b=1$.

3. 存在$x_{0}\in(a,b)$, 使$g’(x_{0})=0$的反例: $f(x)=x^{2}$, $g(x)=x^{3}$,
   $x\in[-1,1]$.

反例: 洛必达法则失效的极限.

$$\lim_{x\to0}\frac{x^{2}\sin\frac{1}{x}}{\sin x}.$$

反例: 对于任意的$x\in(a,b)$, 有$f’(x)>0$, 则函数$f(x)$在$(a,b)$内严格增加. 反之不成立.

$f(x)=x^{3}$, $x\in[-1,1]$.

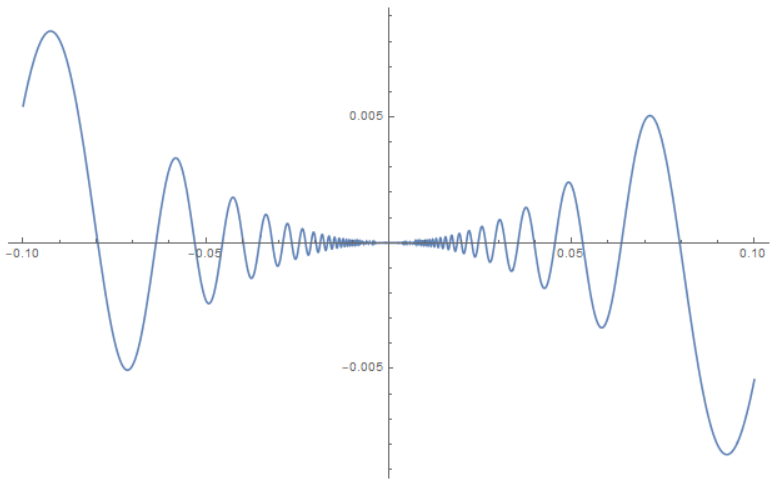
反例: 导数在某点大于零的可微函数, 但在该点的任何领域内都不单调.

$$f(x)=\begin{cases} x+2x^{2}\sin\frac{1}{x}, & x\ne0,\\ 0, & x=0, \end{cases}$$

$$f'(x)=\begin{cases} 1+4x\sin\frac{1}{x}-2\cos\frac{1}{x}, & x\ne0,\\ 1, & x=0, \end{cases}$$

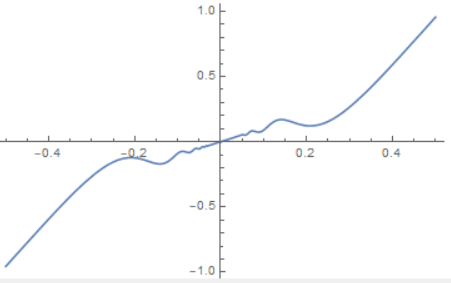
有$f’(0)=1>0$, 但$f’(x)$在$x=0$附近符号高频变动.

反例: 若函数$f(x)$在$(a,+\infty)$内可导, 且$\lim_{x\to+\infty}f’(x)=A$, 则$\lim_{x\to+\infty}\frac{f(x)}{x}=A$. 反之不对.

$f(x)=\sin x$, $x\in(a,+\infty)$. 大多数有界周期函数.

反例: 函数$f(x)$的极值点必是稳定点. 反之不对.

$f(x)=x^{3}$, $x\in\RR$.

反例: 不可导点可能是极值点.

反例: 函数$f(x)$在$x_{0}$点有极大值, 但在此点领域内$f(x)$不一定在$x_{0}$左侧单调上升, 右侧单调下降的情况.

$$f(x)=\begin{cases} 2-x^{2}\left(2+\sin\frac{1}{x}\right), & x\ne0\\ 2, & x=0 \end{cases}$$

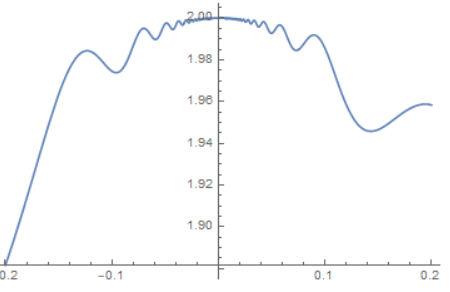
反例: 拐点处不一定有$f’’(x_{0})=0$.

拐点只是凹凸性变化的连接点, 甚至不一定有二阶导数.

反例: 拐点处不一定有切线.

同上

---

reference: 《数学分析中的反例》