勘误列表
发表于|更新于|数学
这里主要收录读书过程中因为证明过程的逻辑漏洞导致的各种障碍, 其中不免会有错误证明或者错误结论.
收录学科方向不限, 会指明出处, 并尽可能给出版次.
问题1: 设$f(x)$是$\RR$上的有界实函数, 且
试求出$f$的较小的正周期.
原证明

反例的构造
错误点: 方程化为
记$F(x)=f\left(x+\frac{1}{6}\right)-f(x)$, 则$F$有周期$T=\frac{1}{7}$.
但证明过程中不应当能得到
不然, 将能够证明$f$有周期$\frac{1}{42}$.
同样的方法可以证明
如果记上式右边为$H(x)$, 则可以证明$H(x)$有周期$1$, 从而由$f$的有界性, $H$恒为零. $f$也有周期为$1$.
现在需要给出反例说明, 存在函数$f$的最小正周期为$1$, 而不能是$\frac{1}{42}$, 这样就从根本上推翻了上面的证明,
而不是因为没能理解, 可能结论仍是对的的嫌疑.
由于已经证明了$f$有周期$1$, 所以只要在$[0,1]$上考虑问题. 将$[0,1]$区间分成$42$份, 每份上附上一个未知数, 如下
1 | (f[#/42] = a[#]) & /@ Range[0, 41]; |
上面要解的方程刚好$42$个, 对应于把区间分成$42$份, 每份赋值为$a[i]$这$42$个未知数. 但由于递推式中各项系数之和是$0$, 所以尽管有$42$个未知数对应$42$个(齐次)方程, 但方程很大可能是没有唯一解的.
1 | Solve[And @@ Join[d1, d2, d3, d4], Table[a[i], {i, 0, 41, 1}]] |
上面的代码给出, $42$个方程的解有$12$个自由变量. 验证方程的系数矩阵的秩给出的结果也是$30$, 如下:
1 | {b,A} = CoefficientArrays[Join[d1, d2, d3, d4], |
所以尝试对$a[i]$的前$12$变量随机赋值为$i$, 解出所有变量$a[i]$:
1 | sol = Solve[ |
最后按照前面的定义, 将函数$f(x)$重定义并绘图如下
1 | Clear[f]; |
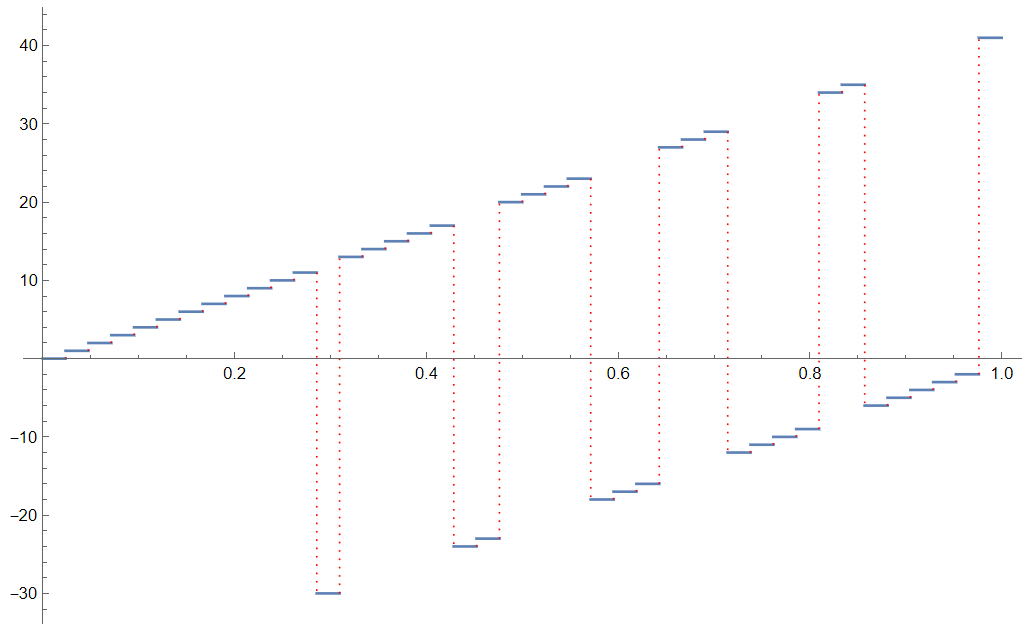
从图像上可以看出, 这样的$f$最小正周期不能小于$1$.
Reference
1. 裴礼文. 数学分析中的典型问题与方法. 高等教育出版社, 1993. ↩
文章作者: Larry Eppes
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Larry_Eppes's Trivia Collection Site!
相关推荐
评论
ValineGitalk
公告
这是 Larry Eppes 的 blog, 仅做一些日常记录.










