数学中的各种图形绘制

笛卡尔叶形线^MSE4435438

ContourPlot[x^3 + y^3 == 3 x*y, {x, -2, 2}, {y, -2, 2},
 Frame -> False(*去除边框*),
 Axes -> True,
 Ticks -> {{2^(2/3)}, {}}(*仅添加横坐标的一个刻度*),
 ContourStyle -> {Thickness[0.007], Dashed, Black}(*等高线样式*),
 Epilog -> {{Red, Line[{{{-2, 1}, {2, -3}}, {{-2, -2}, {3/2, 3/2}}}]},
   {Thickness[0.005], Line[{{2^(2/3), 2^(1/3)}, {2^(2/3), 0}}]},
   PointSize[Large], Point[{3/2, 3/2}],
   Text["(3/2,3/2)", {3/2, 3/2}, {-1.4, -0.5}]}]

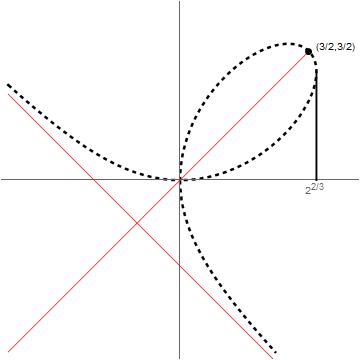
Module[{pt1 = {3/2, 3/2}, pt2 = {2^(2/3), 2^(1/3)}, 
  pt3 = {2^(2/3), 0}}, 
 PolarPlot[
  3 Sin[t] Cos[t]/(Sin[t]^3 + Cos[t]^3), {t, -\[Pi]/4, 7 \[Pi]/4}, 
  PlotRange -> {{-2, 2}, {-2, 5/3}}, 
  PlotStyle -> {Thickness[1/120], Black}, Axes -> True, Ticks -> None,
   AxesStyle -> Directive[Thickness[1/300]], 
  Epilog -> {PointSize[1/50], Thickness[1/200], Point[pt1], 
    Line[{{pt2, pt3}, {pt1, {-1, -1}}, {{-3, 2}, {2, -3}}}]}, 
  ImageSize -> 512]]

^MSE4435438. https://math.stackexchange.com/questions/4435438 ↩

MSE2682544

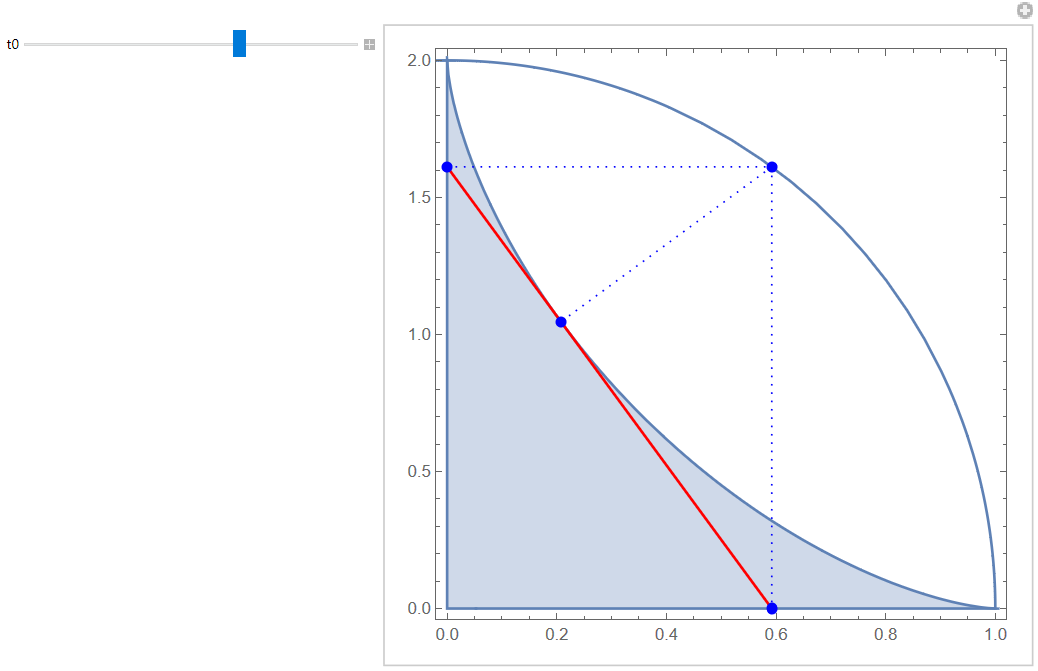
曲线${\left(\frac{x}{a}\right)}^{2/3}+{\left(\frac{y}{b}\right)}^{2/3}=1$上每个点处的切线与坐标轴的截距分别为$h,k$, 则$h,k$满足方程

$$\frac{h^2}{a^2}+\frac{k^2}{b^2}=1.$$

Manipulate[
 Block[{a = 1, b = 2}, 
  h = (a Cos[t0] b Sin[t0]^3 + b a Cos[t0]^3 Sin[t0])/(b Sin[t0]); 
  k = -((2/(3 a Cos[t0]))/(2/(3 b Sin[t0]))) (-a Cos[t0]^3) + 
    b Sin[t0]^3;
  Show[
   {RegionPlot[(x/a)^(2/3) + (y/b)^(2/3) < 1, {x, 0, a}, {y, 0, b}],
    ParametricPlot[{(a Cos[t] b Sin[t]^3 + b a Cos[t]^3 Sin[t])/(
      b Sin[t]), -((2/(3 a Cos[t]))/(2/(3 b Sin[t]))) (-a Cos[t]^3) + 
       b Sin[t]^3}, {t, 0, Pi}],
    Plot[{-((2/(3 a Cos[t0]))/(2/(3 b Sin[t0]))) (x - a Cos[t0]^3) + 
       b Sin[t0]^3}, {x, 0, (
      a Cos[t0] b Sin[t0]^3 + b a Cos[t0]^3 Sin[t0])/(b Sin[t0])}, 
     PlotStyle -> Red],
    Graphics[{Dotted, Blue, Line[{{0, k}, {h, k}, {h, 0}}], 
      Line[{{h, k}, {a Cos[t0]^3, b Sin[t0]^3}}], PointSize[0.02], 
      Point[{{0, k}, {h, 0}, {h, k}, {a Cos[t0]^3, b Sin[t0]^3}}]}]
    }
   ]
  ], {t0, 0.3, Pi/2 - 0.3}
 ]

图像类似这样